Note: Before reading this tutorial you should familiar with the Canvas API. It is simply the best tutorial on HTML5 canvas.

The problem

Even if HTML5 offers support to draw lines, rectangles and other basic shapes, it lacks the option to paint a single point. Point support is vital as is the base of any geometrical system.

There are a few option to simulate a point in HTML5 and here they are:

Solution 1: Draw as tiny line

The basic option is to paint it as very small line. Let's say we want to paint a point at (x,y) coordinates. If you place a grid on canvas then the coordinates on canvas are the intersection of the grid system.

In the image bellow if you want to paint the point at (2,1) you will like to pain the red highlighted pixel but when you specify (2, 1) as coordinates in canvas context it will refer to the grid intersection at (2, 1) 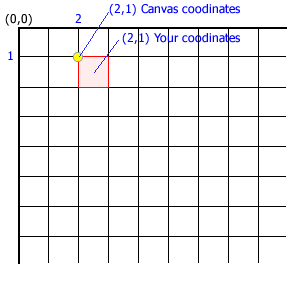So if you want to paint the highlighted pixel you need to paint a line from (2,1) to (3,2).

Here is the code that does that:

ctx.beginPath(); ctx.moveTo(2,1); ctx.lineTo(3,2); ctx.stroke();
A lot complications can appear because:
  • the geometrical coordinates we were taught in math is a little different than the one in canvas
  • this is a solution to paint a pixel my moving to South East but we can have similar solutions by moving South West or North West and so on. Also we can make the number of pixels smaller by painting only North, South, West or East...but this is more close to painting the point as a rectangle.
  • On the edges of the canvas you are not able to paint a line anymore as it might get out of canvas paint surface. Ex: a canvas of 400x400 and you want to paint at (400,1); as (401,2) point is not present on canvas surface the line will be missing (or better said, even if painted not visible)
You can find the whole code for here ( point-as-line.html)

Solution 2: Draw as a tiny rectangle

Another option is to paint the point as rectangle with 1x1 dimension. The code is very similar to the one of "Draw as tiny line". Also the problems are similar

You simply draw a rectangle from point (2,1) with the width of 1 pixel and height of 1 pixel.

ctx.strokeRect(2,1,1,1);
but a better way is to use fill option as this will force the render engine to pain ONLY 1 pixel - the inner one - instead of walking on the edges of the rectangle and do approximations.
ctx.fillRect(2,1,1,1);
You can find the whole code for here ( point-as-rectangle.html)

Solution 3: Draw as tiny circle

We can also paint a point as small circle or ellipse. As a circle has a radius we need to pick the smallest one which is 1 pixel so we will have a circle with 1 as radius which means that the diameter will be 2 pixels - not such a nice idea.

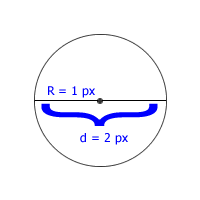Here is the code for this

ctx.beginPath(); ctx.arc(2, 1, 1, 0, 2 * Math.PI, true); ctx.stroke();

A better way to do it - similar to rectangle - is to fill the circle and let the render engine pick only the inner pixel(s).

ctx.beginPath(); ctx.arc(2, 1, 1, 0, 2 * Math.PI, true); ctx.fill();
You can find the whole code for here ( point-as-circle.html)

General problems with these solutions

Most of these problems are problems we encountered when we developed the basic geometrical kernel for Diagramo - so they are real problems.

Zoom In / Out

One of the biggest problem with this solution appear when you want to zoom a point. If that point is a circle and you zoom in, that circle has to be filled, otherwise I will render as an empty circle - a thing you do not want to happen.

Storage of point

If you have an animation, you need to keep track of the points position over time - so you need to store those positions and transformations. For that you will need to use some form of data structure to save the Point for later usage and be able to proper render it.

Skew / distort figure

Fortunately the point can grow/shrink but it can not be distorted - a point will be a point not matter what transformations you will apply to it. Point, in geometry, does not have any dimension so it's immune to transformations ... but in canvas / 2D it is usually a pixel.

We picked the circle / arc solution as is the most flexible and people usually think about points in terms of very small dots - even that is geometrically wrong :)