Table of contents
Note: Before reading this tutorial you should familiar with the Canvas API.
It is simply the best tutorial on HTML5 canvas.
The problem
HTML5's canvas is awesome. You can draw lines, circles. Wow, you can even draw curves, Bézier curves. Quadratic and cubic curves are supported in canvas API.
Awesome! Now, let draw curve through 6 points. Ups, not possible.
That is the dead end I encountered while trying to draw connectors for the flowchart software I play with. They (connectors) can have more than 3 or 4 points so Quadratic and Cubic curves are out of the question.
Also you can not simply join a few Quadratic or Cubic curves to generate a higher degree curves.
Solution
I looked around for a solution not able to find a proper one so I decided to use my rusty old math skills and see if I can find a solution.
Long story short, I did find one (after 2 weeks) and here it is.
Not that my solution can be applied to N grade (N number of points) but it works for Quadratic and Cubic curves too.
Each Bézier curve is actually a parametric curve, a curve that depends on a parameter t, 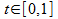 If you vary t in very small steps you will be able to find the proper x an y coordinates.
If you vary t in very small steps you will be able to find the proper x an y coordinates.
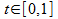 If you vary t in very small steps you will be able to find the proper x an y coordinates.
If you vary t in very small steps you will be able to find the proper x an y coordinates.
Quadratic curves
I will describe a quadratic (grade 2) by Q(t).
So for Quadratic curve you have 3 points: one start point (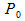 ), one control point (
), one control point (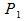 ) and an end point (
) and an end point (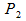 ).
).
 The equation for quadratic curve is:
The equation for quadratic curve is:
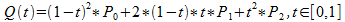 So, the x and y of any point on the curve depends on t like this:
So, the x and y of any point on the curve depends on t like this:
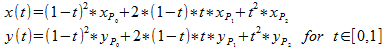
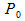 ), one control point (
), one control point (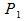 ) and an end point (
) and an end point (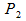 ).
).
 The equation for quadratic curve is:
The equation for quadratic curve is:
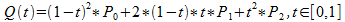 So, the x and y of any point on the curve depends on t like this:
So, the x and y of any point on the curve depends on t like this:
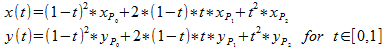
Cubic curves
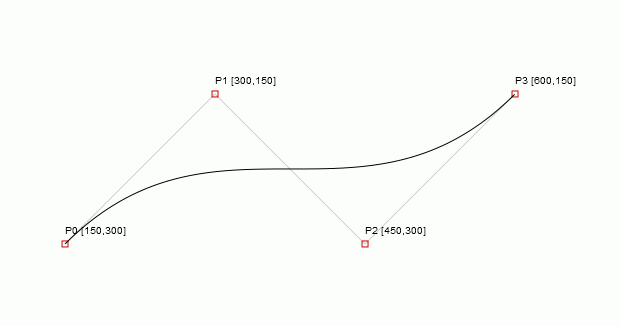
I will describe a cubic (grade 3) curve by C(t)
For cubic curves you have 4 points: one start point (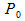 ),
two control points (
),
two control points (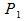 and
and 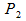 )
and an end point (
)
and an end point (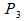 ).
).
 The equation for cubic curve is:
The equation for cubic curve is:
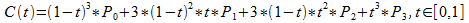 So, the x and y of any point on the curve depends on t like this:
So, the x and y of any point on the curve depends on t like this:
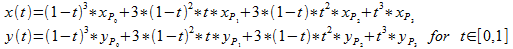
 ),
two control points (
),
two control points (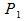 and
and 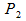 )
and an end point (
)
and an end point (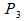 ).
).
 The equation for cubic curve is:
The equation for cubic curve is:
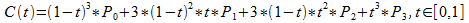 So, the x and y of any point on the curve depends on t like this:
So, the x and y of any point on the curve depends on t like this:
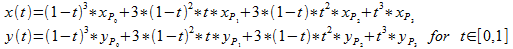
N Grade Bézier curves
I will describe a N grade Bézier curve by B(t).
 Equation for a N grade Bézier curve is:
Equation for a N grade Bézier curve is:
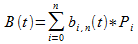
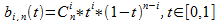
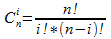 So the x and y for any point on the curve is:
So the x and y for any point on the curve is:
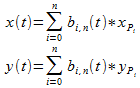 Now, if you vary the t from 0 to 1 you will be able to actually draw the Bézier curve. Not only you can draw the Bézier curve but you can also compute it's nearness, collision or intersections.
The code to do that is pretty simple
Now, if you vary the t from 0 to 1 you will be able to actually draw the Bézier curve. Not only you can draw the Bézier curve but you can also compute it's nearness, collision or intersections.
The code to do that is pretty simple
 Equation for a N grade Bézier curve is:
Equation for a N grade Bézier curve is:
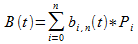
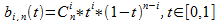
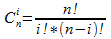 So the x and y for any point on the curve is:
So the x and y for any point on the curve is:
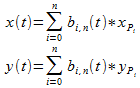 Now, if you vary the t from 0 to 1 you will be able to actually draw the Bézier curve. Not only you can draw the Bézier curve but you can also compute it's nearness, collision or intersections.
The code to do that is pretty simple
Now, if you vary the t from 0 to 1 you will be able to actually draw the Bézier curve. Not only you can draw the Bézier curve but you can also compute it's nearness, collision or intersections.
The code to do that is pretty simple
/**Computes factorial*/
function fact(k){
if(k==0 || k==1){
return 1;
}
else{
return k * fact(k-1);
}
}
/**Computes Bernstain
*@param {Integer} i - the i-th index
*@param {Integer} n - the total number of points
*@param {Number} t - the value of parameter t , between 0 and 1
**/
function B(i,n,t){
//if(n < i) throw "Wrong";
return fact(n) / (fact(i) * fact(n-i))* Math.pow(t, i) * Math.pow(1-t, n-i);
}
/**Computes a point's coordinates for a value of t
*@param {Number} t - a value between o and 1
*@param {Array} points - an {Array} of [x,y] coodinates. The initial points
**/
function P(t, points){
var r = [0,0];
var n = points.length-1;
for(var i=0; i <= n; i++){
r[0] += points[i][0] * B(i, n, t);
r[1] += points[i][1] * B(i, n, t);
}
return r;
}
Drawing
As you can draw the curve by drawing small enough segments that it will look curve enough for the human eye.
Ok, all that you have to do is to variate t between 0 and 1.
Not so fast.
The problem is to find the proper step for this iteration. For some cases a step of 0.2 will be enough, while for other (long curves) is not.
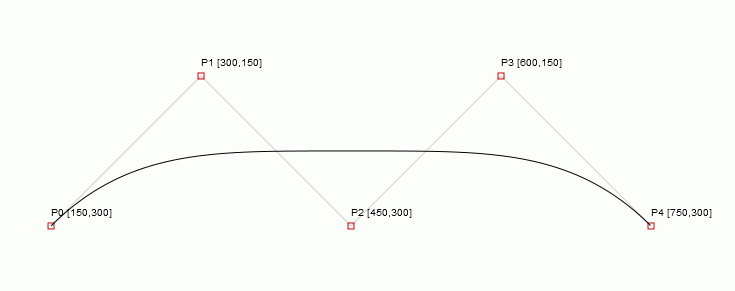
Bellow is a Bézier of grade 5 with a step of 0.2. See the sharp/jagged curve shape.
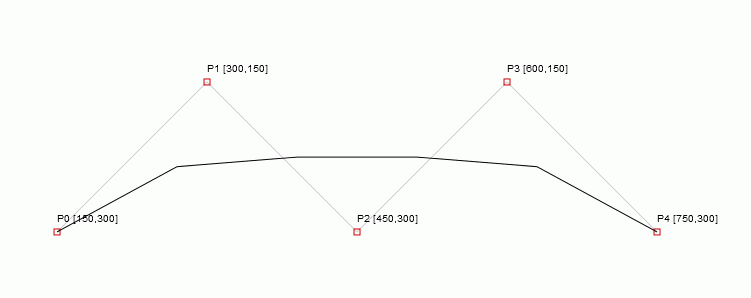 A very rude solution is to compute the length of the polyline P0, P1, P2, ....Pn and use that length to find a proper step (Ex: 1 / length(P0P1...Pn))
The code is again pretty simple:
A very rude solution is to compute the length of the polyline P0, P1, P2, ....Pn and use that length to find a proper step (Ex: 1 / length(P0P1...Pn))
The code is again pretty simple:
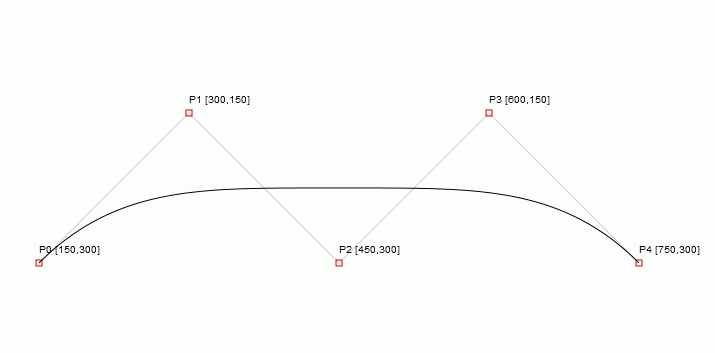 Pretty good; as you can see, the curve is smooth enough. Well it should be, it was drawn using 849 intermediate points.
This solution will produce "good enough" results for rendering but if you are like me and you do not want to let chance play tricks on it there is a better solution:
recursively split the Bezier curves into smaller and smaller pieces until the distance between 2 adjacent point is no greater than 1 - which means 1 pixel.
This means that the number of points will not be evenly distributed among the 0 to 1 interval.
This will be covered in a following article.
Pretty good; as you can see, the curve is smooth enough. Well it should be, it was drawn using 849 intermediate points.
This solution will produce "good enough" results for rendering but if you are like me and you do not want to let chance play tricks on it there is a better solution:
recursively split the Bezier curves into smaller and smaller pieces until the distance between 2 adjacent point is no greater than 1 - which means 1 pixel.
This means that the number of points will not be evenly distributed among the 0 to 1 interval.
This will be covered in a following article.
 A very rude solution is to compute the length of the polyline P0, P1, P2, ....Pn and use that length to find a proper step (Ex: 1 / length(P0P1...Pn))
The code is again pretty simple:
A very rude solution is to compute the length of the polyline P0, P1, P2, ....Pn and use that length to find a proper step (Ex: 1 / length(P0P1...Pn))
The code is again pretty simple:
function distance(a, b){
return Math.sqrt(Math.pow(a[0]-b[0], 2) + Math.pow(a[1]-b[1], 2));
}
/**Compute the incremental step*/
var tLength = 0;
for(var i=0; i< points.length-1; i++){
tLength += distance(points[i], points[i+1]);
}
var step = 1 / tLength;
//compute the support points
var temp = [];
for(var t=0;t<=1; t=t+step){
var p = P(t, points);
temp.push(p);
}
return temp;
Bellow see the "rude" solution in action:
 Pretty good; as you can see, the curve is smooth enough. Well it should be, it was drawn using 849 intermediate points.
This solution will produce "good enough" results for rendering but if you are like me and you do not want to let chance play tricks on it there is a better solution:
recursively split the Bezier curves into smaller and smaller pieces until the distance between 2 adjacent point is no greater than 1 - which means 1 pixel.
This means that the number of points will not be evenly distributed among the 0 to 1 interval.
This will be covered in a following article.
Pretty good; as you can see, the curve is smooth enough. Well it should be, it was drawn using 849 intermediate points.
This solution will produce "good enough" results for rendering but if you are like me and you do not want to let chance play tricks on it there is a better solution:
recursively split the Bezier curves into smaller and smaller pieces until the distance between 2 adjacent point is no greater than 1 - which means 1 pixel.
This means that the number of points will not be evenly distributed among the 0 to 1 interval.
This will be covered in a following article.
Download
As canvas does not support this option I added a patch so you can use it to draw your curves.
You can download whole code from here
 HTML5 Tutorial: How to draw n grade Bézier curve with Canvas API
HTML5 Tutorial: How to draw n grade Bézier curve with Canvas API