Table of contents
The problem
Most of the time just drawing a simple Bézier curve is not enough. You need to join together a few curves to create a complex shape.
I encountered this problem while coding for Diagramo and tried to solve it. (Took me ages to de-rust my math skills)
An option might be to draw n grade Bézier curve for complex shapes but most of the time we are not so lucky to squeeze our shapes even into a single complex curve.
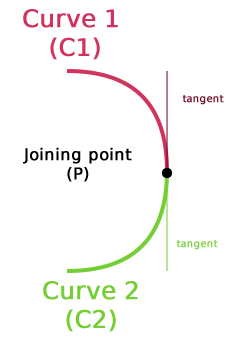
Here are a few example of bad joins. I just added the tangents at joining points so later I can better explain the problem.


Solution
There are two levels of smoothness. First level just makes the transition from one curve to another to look decent while second level make the transition look natural.
Level 1 smoothness
First level of smoothness is reached when the tangent on joining points of the curves are equals.
 As you can see the tangent of those 2 curves coincide and the transition is smoother.
Mathematically this means that the first derivative of first curve must be equal to the first derivate of the second one (at the glue point) :
As you can see the tangent of those 2 curves coincide and the transition is smoother.
Mathematically this means that the first derivative of first curve must be equal to the first derivate of the second one (at the glue point) :
 In the Formulas section you will find the formulas for Cubic, Quadratic curves and their first derivatives.
So all you have to do is to solve those equations (or keep them valid – in case you do something dynamic)
Even if now the curves join together nicely the join still looks "unnatural". That is because the curvature of those 2 curves do not coincide in joining point.
In the Formulas section you will find the formulas for Cubic, Quadratic curves and their first derivatives.
So all you have to do is to solve those equations (or keep them valid – in case you do something dynamic)
Even if now the curves join together nicely the join still looks "unnatural". That is because the curvature of those 2 curves do not coincide in joining point.
 As you can see the tangent of those 2 curves coincide and the transition is smoother.
Mathematically this means that the first derivative of first curve must be equal to the first derivate of the second one (at the glue point) :
As you can see the tangent of those 2 curves coincide and the transition is smoother.
Mathematically this means that the first derivative of first curve must be equal to the first derivate of the second one (at the glue point) :
 In the Formulas section you will find the formulas for Cubic, Quadratic curves and their first derivatives.
So all you have to do is to solve those equations (or keep them valid – in case you do something dynamic)
Even if now the curves join together nicely the join still looks "unnatural". That is because the curvature of those 2 curves do not coincide in joining point.
In the Formulas section you will find the formulas for Cubic, Quadratic curves and their first derivatives.
So all you have to do is to solve those equations (or keep them valid – in case you do something dynamic)
Even if now the curves join together nicely the join still looks "unnatural". That is because the curvature of those 2 curves do not coincide in joining point.
Level 2 smoothness
In order to make the the join more natural you have to have first derivate (tangent) and second derivative (curvature) equal.
 These conditions ensure that the transition from a curve to the next is smooth and natural.
These conditions ensure that the transition from a curve to the next is smooth and natural.

 These conditions ensure that the transition from a curve to the next is smooth and natural.
These conditions ensure that the transition from a curve to the next is smooth and natural.
Formulas
Quadratic curve
The equation for Quadratic (Q(t)) is
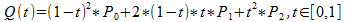 with start point (
with start point (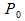 ), one control point (
), one control point (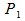 ) and an end point (
) and an end point (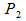 ) .
Derivative formulas are:
) .
Derivative formulas are:
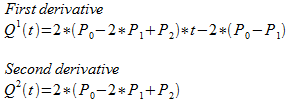
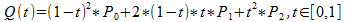 with start point (
with start point (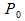 ), one control point (
), one control point (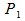 ) and an end point (
) and an end point (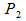 ) .
Derivative formulas are:
) .
Derivative formulas are:
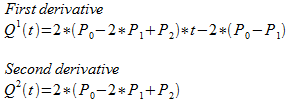
Cubic curve
The equation for Cubic (C(t)) curves is
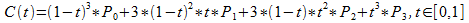 with one start point (
with one start point (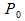 ), two control points (
), two control points (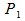 and
and 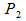 ) and an end point (
) and an end point (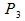 ).
Derivative formulas are
).
Derivative formulas are
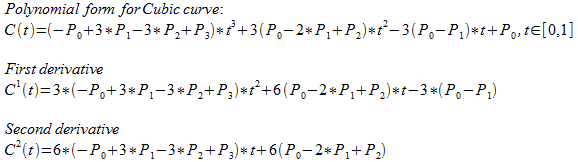
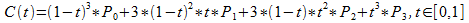 with one start point (
with one start point (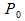 ), two control points (
), two control points (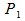 and
and 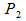 ) and an end point (
) and an end point (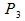 ).
Derivative formulas are
).
Derivative formulas are
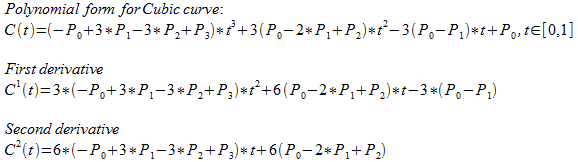
 HTML5 Tutorial: How to join two bezier curves with the canvas API
HTML5 Tutorial: How to join two bezier curves with the canvas API